Ordenadores Paralelos de memoria distribuída.

Los problemas de cálculo computacional que se suelen encontrar en las aplicaciones científicas y de ingeniería suelen presentar unas dimensiones muy elevadas. Resolver estos problemas utilizando ordenadores convencionales puede consumir demasiado tiempo de proceso y demandar demasiada cantidad de almacenamiento. En muchos casos, los procesadores paralelos de memoria distribuida (DM-MIMD: MIMD son las iniciales de multiple instruction, multiple data) pueden proporcionar tanto la potencia de cálculo como la cantidad de memoria necesaria para resolver este tipo de problemas.

Arquitectura de Ordenandores DM-MIMD.

• Grafos
• Arrays, anillos y toroides.
• Rendimiento de las comunicaciones en los ordenadores DM-MIMD.
• Paso de mensajes entre nodos vecinos.
• Paso de mensajes entre nodos arbitrarios.
• Paso de mensajes largas.
• La contención en los enlaces de comunicación.
• Rendimiento global de ordenadores DM-MIMD.

Arquitectura de ordenadores DM-MIMD

Un DM-MIMD es un ordenador paralelo en el cual cada procesador tiene acceso directo únicamente a su memoria local. Los procesadores se encuentran interconectados mediante enlaces de comunicación, y los procesadores intercambian los datos en forma de mensajes que se distribuyen a través de estos enlaces. Debido a que un DM-MIMD está formado por ordenadores MIMD, es posible ejecutar múltiples programas en cada procesador de forma simultánea.

Los distintos tipos de ordenadores paralelos DM-MIMD se puede caracterizar atendiendo a diversos factores como: la potencia de los procesadores, el tamaño de la memoria, la velocidad de las comunicaciones entre los procesadores, la disponibilidad de medios de entrada/salida, y el patrón de interconexión entre los procesadores. Los ordenadores DM-MIMD pueden estar formados por tan sólo dos procesadores o por varios miles de procesadores. Estos procesadores pueden estar conectados formando un anillo, mallas bidimensionales ó formas toroidales, entre otras estructuras.

Grafos de interconexión.

Los nodos en los ordenadores DM-MIMD se pueden representar como los nodos de un grafo determinado, y los enlaces utilizados en las comunicaciones entre los procesadores se encuentran en los bordes de este grafo. A continuación se muestran algunos de los tipos de grafos más importantes que se utilizan en los DM-MIMD comerciales.

Arrays, anillos y toroides

La figura 1 muestra los grafos más sencillos que se pueden encontrar en los ordenadores DM-MIMD. El diagrama (a) representa una matriz lineal de ocho procesadores. En esta distribución, un nodo tiene uno o dos vecinos más cercanos, dependiendo de si se encuentra en uno de los extremos de la matriz. Si se unen los extremos de este array, se obtiene un anillo, tal y como se muestra en el diagrama (b). En este caso, todos los nodos tienen dos vecinos.

Los nodos también se pueden conectar formando un array bidimensional de p1 ´ p2 elementos, ó una malla de procesadores, como se muestra en el diagrama (c). En este caso, p1 = 2 y p2 = 4, y cada nodo tiene dos o tres vecinos, en función de su posición en la malla. En una malla con más filas, un nodo puede tener hasta cuatro vecinos más cercanos. Estos vecinos se identifican por sus posiciones relativas y se denominan vecinos norte, sur, este y oeste 

Si se conectan los nodos correspondientes a los extremos izquierdo y derecho y los correspondientes a los extremos superior e inferior de una malla bidimensional, ésta se convierte en un torus tridimensional como se muestra en el diagrama (d). En este caso, todos los nodos tienen cuatro vecinos más próximos.

Al aumentar la conectividad del grafo de ocho procesadores, se reduce la distancia máxima que existe entre dos procesadores cualesquiera del grafo. En un DM-MIMD, esto se traduce en una reducción en el tiempo para realizar las comunicaciones entre procesadores. Así, en un array lineal, existen p-1 líneas entre los nodos 0 y el p-1, y éste es el camino más largo entre cualquier par de nodos. Este camino se muestra representado por la flecha del diagrama (a) de la figura 2. Si se conectan los bordes de este array para formar un anillo, se reduce este camino hasta la mitad. Si además se permite que exista comunicación en ambos sentidos (es decir, si el grafo es bidireccional), el camino más largo se encuentra entre los nodos 0 y p/2, y este camino recorre p/2 líneas de comunicación en el diagrama (b) de la figura 1. En la malla, el camino más largo entre nodos se encuentra entre las esquinas opuestas (figura 2(c)). Este camino tiene de longitud p1 + p2 – 2. Cuando p = 8, el camino más largo entre los dos es cuatro, tanto para el anillo como para la malla. Las ventajas de la malla son más evidentes para un número de nodos mayor. Por ejemplo, el camino más largo en una malla de dimensiones 16 ´ 16 recorre 30 líneas de conexión, mientras que el camino más largo en un anillo de 162 = 256 nodos recorre 128 líneas de conexión.

El torus permite unas condiciones todavía más favorables. Puede interpretarse como un conjunto de p1 anillos horizontales de p2 nodos, cada uno de ellos interconectados mediante p2 anillos verticales de p1 nodos cada uno. Por tanto, el camino más largo que debe recorrerse entre el nodo A y el nodo B es, para este ejemplo, la distancia entre el anillo vertical del nodo A y el anillo vertical del nodo B, más la distancia alrededor de éste anillo hasta llegar al nodo B (figura 2(d)). Si cada anillo puede ser recorrido en ambos sentidos, el camino más largo es p1/2 + p2/2. En el toro 2 ´ 4, el camino más largo es tres. En el toro de dimensiones 16 ´ 16, esta distancia es 16.

Rendimiento de las comunicaciones en los ordenadores DM-MIMD

La evolución de los ordenadores ha traído consigo una gran mejora en su rendimiento. Al igual que con cualquier otro tipo de ordenador, el rendimiento de los ordenadores DM-MIMD se puede representar de distintas formas, en función del número de Mflops que alcanza ó el benchmark del LINPACK, por ejemplo. Además de estas medidas de rendimiento clásicas, el rendimiento de un ordenador DM-MIMD está determinado por la velocidad de las comunicaciones de datos entre los nodos. A continuación se muestra cómo esta velocidad de comunicación puede afectar al rendimiento de los ordenadores DM-MIMD.

Paso de mensajes entre nodos vecinos.

Se dice que existe transmisión de mensajes entre dos nodos cuando se ejecuta un comando para enviar un mensaje en el nodo emisor, y se ejecuta un comando de recepción de este mensaje en el nodo receptor. El proceso exacto de paso de mensajes que se realiza después de ejecutarse estos comandos depende de cada ordenador, pero suele involucrar procesos de inicialización de los buffers de mensajes en ambos nodos, así como el establecimiento de la ruta de comunicación entre ellos, además de la transferencia del mensaje actual a través de los enlaces de comunicación.

Si b es el tiempo necesario para preparar el hardware y el software necesario para transmitir un mensaje y t es el tiempo empleado en enviar un byte de datos a través del enlace que une a los dos nodos, el tiempo necesario para enviar k bytes de datos desde un nodo a uno de sus vecinos más cercanos está dado por la expresión:

Tcomun = ß + kt

Normalmente, el tiempo necesario para enviar un mensaje es mucho mayor que el tiempo necesario para realizar un operación en punto flotante. En particular, b >> w ³ t, en donde w es el tiempo necesario para realizar una operación en punto flotante. La tabla 1.11 muestra los valores de b, w, t y la relación b/w para algunos ordenadores DM-MIMD. Todos los tiempos que se muestran están representados en microsegundos. En este tabla, w representa el tiempo necesario para realizar una multiplicación en punto flotante de doble precisión (8 bytes). La primera columna muestra el año en el que se presentó la máquina, aunque algunos datos fueron modificados en los modelos mejorados. La última columna de la tabla muestra la velocidad de reloj de cada procesador.

Cuando la longitud del mensaje es inferior a 100 bytes, en el iPSC/2 y en el iPSC/860 se utiliza un protocolo especial para transmitir mensajes. En estos casos, los valores de b se encuentran reducidos. Los valores de b para estos mensajes pequeños se muestran entre paréntesis dentro de la tabla.

La tabla 1 muestra que tanto la computación como la comunicación con el vecino más próximo han mejorado en rendimiento a medida que han aparecido nuevos ordenadores. Sin embargo, todavía se cumple que b >> t. Esto significa que es mejor enviar muchos bytes de datos en un único mensaje que enviar la misma cantidad de datos utilizando muchos mensajes pequeños. Los programas que se van a ejecutar sobre ordenadores DM-MIMD deben ser diseñados teniendo esto presente.

Paso de mensajes entre nodos arbitrarios

Cuando los nodos de envío y recepción no son los vecinos más cercanos, el coste de la transmisión de los datos depende completamente de cómo los nodos intermedios que se encuentran a lo largo del camino que debe seguir el mensaje manejan esta transferencia de mensajes. Los primeros ordenadores DM-MIMD, como el iPSC/1, tenían un único procesador por nodo. Este procesador se encargaba no sólo del cálculo, sino también de la comunicación, así que los mensajes que llegan a un nodo interrumpen cualquier operación que esté realizando, incluso si ese nodo no es el receptor del mensaje. Los últimos modelos de ordenadores DM-MIMD, a partir del iPSC/2 y el nCUBE/2, tienen hardware específico separado para realizar los cálculos y las comunicaciones, y pueden operar de forma independiente. Los mensajes que pasan a través de un nodo se procesan mediante un procesador de comunicaciones de forma que los cálculos que se estén realizando no se ven afectados. Sin embargo, todavía sigue siendo más costoso enviar un mensaje desde un nodo a otro que se encuentre distante, que enviar el mensaje a nodos que sean vecinos, ya que el mensaje va sufriendo pequeños retrasos al pasar por cada uno de los procesadores intermedios.

El rendimiento en las comunicaciones interprocesadores se ha incrementado con la llegada del wormhole routing. En el wormhole routing (como el implementado en los ordenadores de Intel), se envía un paquete "preliminar" desde el emisor al receptor para configurar y reservar un canal de comunicación a través de los nodos intermedios. El mensaje pasa entonces a través de ese canal sin retardos. El overhead debido a este mecanismo de switching de circuitos es difícil de medir, pero parece representar sólo un pequeño porcentaje del tiempo total de comunicación en las nuevas máquinas (como en los ordenadores de Intel: Delta y Paragon). Por tanto, en ordenadores con wormhole routing, el tiempo necesario para enviar un mensaje entre nodos distantes es aproximadamente el mismo que el tiempo necesario para enviarlo a nodos vecinos.

La velocidad de la comunicación entre nodos se refleja en el ancho de banda de comunicación de una máquina: cuando la velocidad de transferencia es rápida, se transmiten un mayor número de bytes de datos por segundo. La tabla 2 muestra el ancho de banda de comunicación de varios multiprocesadores medido en función del tamaño del mensaje (8, 1024 y 8192 Kbytes) y la distancia que debe viajar en el ordenador. Un mensaje de tipo "1 hop" representa un mensaje entre los vecinos más próximos, y un mensaje "6 hop" es un mensaje que pasa a través de cinco nodos intermedios que se encuentran entre el emisor y el receptor. Las máquinas que no poseen procesadores separados de comunicación o que no permiten hacer wormhole routing (como el iPSC/1 y el nCUBE/1) sufren una fuerte degradación en su ancho de banda cuando el número de hops aumenta desde uno hasta 6. Los otros ordenadores demuestran poca o ninguna disminución en el ancho de banda de comunicación entre nodos distantes.

Paso de mensajes largas.

En la expresión que mostramos para Tcomun, el tamaño del mensaje sólo aparece dentro del término kt. Sin embargo, en la mayoría de los ordenadores el tiempo de arranque b (startup) también suele ser función del tamaño del mensaje.

Tal y como se recoge en la tabla 1, el tiempo de startup se reduce en el iPSC/2 y en el iPSC/860 cuando k es muy pequeño. En algunos ordenadores b también aumenta cuando el tamaño del mensaje es muy grande. En este caso, el mensaje puede ser enviado como un conjunto de paquetes más pequeños en vez de cómo un mensaje único más grande, y el envío de cada paquete individual sólo añade una pequeña cantidad de coste adicional a la comunicación completa. A pesar de que la mayoría del tiempo de arranque (startup) se utiliza para el primer paquete, el efecto de dividir el mensaje en paquetes (empaquetamiento) suele hacerse visible en una representación en la que se muestre el tiempo de comunicación entre dos nodos frente al tamaño del mensaje. La figura 3 muestra esta representación para dos ordenadores hipotéticos, uno que divide los mensajes grandes en paquetes y otro que no los divide. La línea sólida muestra Tcomun = b + kt representada en función de t cuando b = 500 y t = 1 para un ordenador que no realiza empaquetamiento. Como era de esperar, esta gráfica es una función lineal de k. La pendiente de esta recta es t, y su punto de corte con el eje Y coincide con b.

Como contraste, la línea punteada de la figura 3 muestra la forma característica de la curva cuando el mensaje se divide en paquetes de 250 bytes de longitud. Las líneas sólida y punteadas con colineales hasta que k = 251. En este punto, el ordenador que realiza empaquetamiento divide el mensaje en dos paquetes: uno con 250 bytes y otro con el byte restante. El repentino salto en la cantidad de tiempo refleja el overhead necesario para enviar el segundo paquete; la curva aumenta a continuación de forma lineal mientras el segundo paquete crece hasta los 250 bytes. Cuando k = 501, la curva muestra otro salto, debido a que es necesario enviar un tercer paquete. A pesar de que los gráficos obtenidos a partir de resultados experimentales no suelen ser tan "suaves" como los mostrados en la figura 3, la forma en escalón de la curva punteada tiende a aparecer claramente al realizar las medidas en ordenadores que presentan un overhead de empaquetamiento medible. En particular, se puede observar este comportamiento en los programas reales en los que intervengan mensajes de longitud elevada. El tamaño del paquete suele ser moderadamente grande: en el iPSC/1 es de 1024 bytes, en el Delta es de 476 bytes, y en el Paragon es de 1792 bytes.

El overhead debido al empaquetamiento de mensajes es evidente en los anchos de banda que se muestran en la tabla 2. En concreto, el empaquetamiento de los mensajes significa que no se observa el aumento lineal en el ancho de banda que se esperaría a partir de la dependencia lineal de Tcomun con el tamaño del mensaje. Este efecto aparece en los datos de 1-hop del nCUBE/2. Cuando el tamaño del mensaje aumenta desde 8 hasta 1024 bytes (por un factor de 128), el ancho de banda en la comunicación con el vecino más próximo aumenta desde 50 Kb/s hasta 1289 Kb/s (un factor de tan sólo 26). Al aumentar el tamaño del mensaje desde 1024 hasta 8192 (un factor de 8) sólo aumenta el ancho de banda en un factor de 1.2. Sin embargo, incluso aunque se pierda eficiencia en el proceso de empaquetamiento, el incremento en ancho de banda en conjunto con el aumento de la longitud del mensaje demuestra que es generalmente preferible pasar sólo unos pocos mensajes largos que pasar muchos mensajes pequeños.

La contención en los enlaces de comunicación.

Un último aunque muy importante aspecto del rendimiento en las comunicaciones entre nodos es el número de mensajes que recorren una determinada línea de comunicación en un momento dado. Cuando más de un mensaje atraviesa un circuito de comunicación dado, se dice que estos mensajes compiten por ese circuito. Los efectos de esta contención dependen del ordenador en el que se produzcan. Por ejemplo, si nodos vecinos de un iPSC/1 mandan mensajes a cada uno de forma simultánea, el tiempo necesario para el intercambio de datos es aproximadamente 2Tcomun: ni los tiempos de inicialización (startup) ni las transferencias de datos a través del enlace pueden solaparse. Sin embargo, los últimos modelos de ordenadores paralelos sí permiten que las inicializaciones para la emisión y recepción de mensajes se solapen en el tiempo, y el tiempo necesario para esta transmisión (denominada head-to-head send) se aproxima a b + 2kt.

El problema de la contención se complica cuando los mensajes que se envían entre varios nodos toman caminos desconocidos a través del ordenador paralelo. Por ejemplo, supongamos que un mensaje de k-bytes se encuentra retrasado, mientras que un conjunto de mensajes de q bytes pasa a través de un enlace hacia su camino. Entonces, el tiempo que necesita ese mensaje para llegar a su destino se ve incrementado en un factor qt. Si q es grande, este retraso puede ser sustancial. La contención se produce en un enlace de comunicación siempre que la cantidad de datos total que debe pasar a través de él supera el ancho de banda de ese enlace.

El efecto global de la contención sobre el rendimiento de un programa paralelo resulta muy difícil de predecir, pero, en general, resulta conveniente programar de forma que se eviten las posibles contenciones.

Rendimiento global de ordenadores DM-MIMD

El rendimiento global de los ordenadores paralelos de tipo DM-MIMD está determinado no sólo por su rendimiento en las comunicaciones sino también por su rendimiento computacional. La tabla 1 mostraba que, al igual que sucedía con el tiempo necesario para enviar un mensaje, el tiempo necesario para realizar una multiplicación en punto flotante de doble precisión también ha disminuido sustancialmente con cada nueva arquitectura. Esto también es cierto para el tiempo necesario para cualquier otra operación en punto flotante. Así pues, dado que la velocidad de comunicación y la velocidad de cálculo han aumentado, debemos suponer que un programa paralelo se ejecutará de forma más rápida en un modelo nuevo de ordenador DM-MIMD que en un modelo anterior.

Sin embargo, la velocidad de ejecución no es el único ingrediente necesario para mejorar el rendimiento. La Ley de Amdahl nos dice que el speedup de un programa paralelo se encuentra limitado por la fracción de tiempo que se consume en realizar operaciones que no se pueden ejecutar en paralelo. Por extensión, el speedup también se encuentra limitado por el tiempo necesario para realizar la comunicación de datos. Dado que no se realizan comunicaciones cuando un programa se ejecuta en un único nodo, la comunicación constituye una parte del overhead propio de la implementación paralela.

Para poder apreciar el efecto de la comunicación de datos sobre el speedup, podemos suponer que tenemos un programa secuencial con cálculos perfectamente paralelizables. Si no se necesitase ningún tiempo para realizar las comunicaciones entre los nodos, el tiempo necesario para ejecutar el programa sobre p nodos sería sólo el tiempo necesario para ejecutar el programa en un único nodo y dividido por p, es decir, Tp = T1/p. Si se necesita realizar comunicaciones de datos, y las comunicaciones y los cálculos no se pueden solapar en el tiempo, el tiempo necesario para realizar el cálculo en p-nodos aumenta en un factor Tc, necesario para realizar las comunicaciones, de forma que 

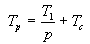
Teniendo en cuenta que el speedup para un programa paralelo se define como 

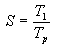
Para poder examinar más fácilmente los efectos de la comunicación sobre el speedup, podemos considerar el valor recíproco

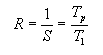
Para nuestro programa "perfecto" con comunicaciones de datos, este recíproco se convierte en

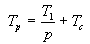
Si el coste de comunicaciones es nulo, entonces R = 1/p y el programa presenta un speedup perfecto S = p. En cualquier otro caso, el recíproco del speedup está determinado por la relación Tc/T1. Cuanto mayor sea el coste debido a las comunicaciones en comparación con el coste computacional (o de cálculo), mayor será el valor de R. Por tanto, cuanto mayor sea la relación de los costes de comunicación en comparación con los costes de computación, menor será el speedup S. La última columna de la tabla 1 muestra la relación del tiempo para la inicialización del mensaje b con el tiempo necesario para realizar una operación de multiplicación en punto flotante w. Estos datos muestran claramente que con el incremento en la velocidad de cálculo, se ha producido un marcado incremento en la relación entre el coste de comunicación y el coste de cálculo. Por tanto, aunque podemos esperar que nuestro programa paralelo se ejecute mucho más rápidamente sobre estos nuevos ordenadores, también podemos esperar que el speedup que obtengamos sea inferior.

El incremento en la relación entre comunicaciones y cálculo, ha cambiado recientemente debido a la mejora sustancial en las capacidades de comunicación de los nuevos ordenadores DM-MIMD. Entre el iPSC/1 y el Paragon (SUN-MOS), la relación b/w ha crecido en un factor de 66. Al mismo tiempo, el ancho de banda de las comunicaciones para los mensajes de 8192 bytes de longitud ha aumentado en un factor de 164.

Para comprobar las repercusiones que estas mejoras han producido es necesario examinar algunos ejemplos computacionales. Ya que no existen datos estándar del speedup para un gran número de ordenadores, es necesario examinar el speedup de un programa numérico paralelo en comparación con el rendimiento pico teórico del ordenador; aún así, éste es un tipo de medida de la eficiencia poco satisfactoria, ya que mezcla aspectos relacionados con la programación eficiente sobre un único procesador con aspectos de programación paralela, pero de ningún modo nos ofrece una información precisa sobre las tendencias en el speedup, como se comenta a continuación.

El programa paralelo que se ha empleado consiste en la solución del sistema lineal más grande que puede caber en un ordenador DM-MIMD dado: Highly Parallel Computing benchmark (Dongarra, 1994). La tabla 3 muestra el tamaño del sistema n (número de ecuaciones), los megaflops medidos para la solución de ese sistema, y el rendimiento pico teórico de ese ordenador para operaciones aritméticas de 64 bits. La columna final muestra la relación entre el rendimiento medido y el rendimiento pico teórico. Los datos se muestran para ordenadores con p = 1, 2 y 8 nodos.

El iPSC/860 fue uno de los primeros ordenadores DM-MIMD con el rendimiento suficiente para resolver problemas científicos realistas sobre un número moderado de procesadores. Tanto el iPSC/860 como el Delta utilizan el procesador i860. Entre el iPSC/860 y el Delta, la relación b/w (para mensajes largos) disminuyó, mientras que el ancho de banda para los mensajes aumentó. Como se muestra en la tabla 3, el rendimiento global del Delta es incluso mejor que el del iPSC/860, especialmente al aumentar el número de procesadores.

Si comparamos estos dos ordenadores con el nCUBE/2 observamos que la mejora en las comunicaciones no es enteramente responsable del rendimiento paralelo. Los datos que se obtienen para problemas de dimensiones similares cuando p = 8 muestran que, mientras que el rendimiento pico teórico del Delta es 17 veces el del nCUBE/2, el rendimiento experimental aumenta tan sólo en un factor de 14. Esta proporción se cumple a pesar del hecho de que el ancho de banda de la comunicación para un mensaje de 8192 bytes es casi ocho veces mayor en el Delta que en el nCUBE/2. Esto es debido en parte al aumento en 8 veces de la relación b/w entre los dos ordenadores, pero está todavía más influenciado por la dificultad en programar el procesador i860. Los datos para p = 1 muestran que el rendimiento pico teórico es sustancialmente más realista para el nCUBE/2 que para los ordenadores basados en el i860.

La principal ventaja de los ordenadores DM-MIMD reside en sus memorias distribuidas de elevada capacidad y en su potencia de cálculo cumulativo. El Highly Parallel Computing benchmark demuestra el potencial total de un ordenador paralelo para la resolución de sistemas lineales. Este benchmark nos indica los Gflops obtenidos al resolver el sistema lineal más grande que puede caber en el ordenador utilizando cualquier método numérico estable. La tabla 4 muestra estos rendimiento en Gflops y las dimensiones de los problemas para algunas de las máquinas que acabamos de examinar, al utilizar 128 nodos. En comparación, un Paragon (OSF) de 296 nodos es capaz de obtener 12.5 Glops al resolver un problema de 29400 ecuaciones lineales.

Resumiendo, el rendimiento de un ordenador DM-MIMD depende de una gran variedad de factores que interactúan entre sí. El rendimiento pico teórico depende de aspectos estándar como la cantidad de memoria y la velocidad del procesador. Cuando se deben realizar transferencias de datos, también está determinado por el ancho de banda de las comunicaciones. El speedup que se puede alcanzar depende sobre todo del grado en que el programa secuencial se puede dividir en tareas independientes y paralelas. También depende del número y tamaño de los mensajes que se transmiten y de la relación entre los tiempos de comunicación y de cálculo. Resulta muy difícil poder predecir el rendimiento de un programa real estudiando cualquiera de estos aspectos de forma separada, a pesar de que los datos de rendimiento que acabamos de mostrar demuestran que los ordenadores paralelos DM-MIMD pueden resultar una herramienta muy potente para tratar muchas tareas de cálculo intensivo.