|
Ordenadores Vectoriais
Un ordenador vectorial é unha máquina deseñada especificamente para realizar de forma eficiente operacións nas que se ven involucrados elementos de matrices, denominados vectores. Estes ordenadores resultan especialmente útiles para ser empregados no cálculo científico de alto rendemento (high performance computing), onde as operacións con vectores e con matrices son amplamente utilizadas.
Arquitectura xeral
Vectores e aritmética vectorial
Para mostra-los conceptos que se encontran detrás dun procesador vectorial, imos presentar en primeiro lugar unha breve mostra de cómo programar operacións vectoriais sobre códigos FORTRAN.
Un vector v, é unha lista de elementos da forma:
v = (v1, v2, v3,..., vn)T
A lonxitude do vector defínese como o número de elementos no vector, de forma que a lonxitude do vector v que acabamos de presentar é n. Cando queremos representar un vector nun programa, declárase o vector como unha matriz dunha única dimensión. En FORTRAN, declararíamo-lo vector v mediante a expresión:
DIMENSION V (N)
Onde N é unha variable enteira que almacena o valor da lonxitude do vector.
Dous vectores pódense sumar simplemente sumando cada un dos seus compoñentes, é dicir:
s = x + y = (x1+ y1, x2+ y2, . . . , xn+yn)
En FORTRAN, a suma de vectores pódese realizar utilizando o seguinte código:
DO I=1, N
S (I) = X(I) + Y (I)
ENDDO
Onde s é o vector no que se almacena a suma final, e S, X, e Y foron declarados como matrices de dimensión N.
Elementos da arquitectura vectorial
Un ordenador vectorial contén un conxunto de unidades aritméticas especiais denominadas pipelines. Estas pipelines superpoñen a execución das diferentes partes dunha operación aritmética sobre os elementos do vector, producindo unha execución máis eficiente da operación aritmética que se está realizando. En moitos aspectos, unha pipeline é similar a unha cadea de montaxe dunha fábrica de coches, na que os distintos pasos da fase de montaxe dun automóbil, por exemplo, se realizan en distintas etapas da cadea.
Consideremos, por exemplo, os pasos ou etapas necesarias para realizar unha suma nun punto flotante nunha máquina con hardware que empregue aritmética IEEE. Os pasos para realiza-la operación s = x + y son:
- Compáranse os expoñentes dos dous números en punto flotante que se queren sumar para encontrar cál é o número de menor magnitude.
- O punto decimal do número con menor magnitude desprázase de forma que os expoñentes dos números coincidan.
- Súmanse os dous números.
- Normalízase o resultado da suma.
- Realízanse os chequeos necesarios para comprobar se se produciu algún tipo de excepción en punto flotante durante a suma, como un overflow.
- Realízase o redondeo.
A táboa 1. mostra os pasos necesarios para realizar esta suma. Os números que se van sumar son o x = 11234.00 e o y = -567.8. A diferencia da representación habitual, estes números almacénanse en notación decimal cunha mantisa de catro díxitos.
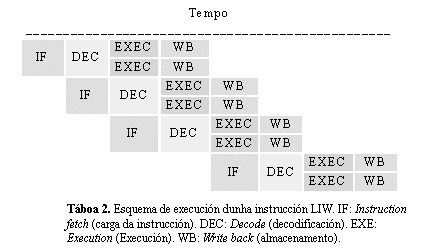
Agora consideremos esta suma escalar realizada sobre tódolos elementos dun par de vectores de lonxitude n. Débense realizar cada unha das seis etapas para cada par de elementos dos vectores. Se en cada fase da execución son necesarias t unidades de tempo, entón cada suma 6t unidades de tempo (sen conta-lo tempo necesario para subministrar e descodifica-la instrucción en si ou para trae-los dous operandos ata a unidade aritmética). Como resultado, o número de unidades de tempo necesarias para sumar tódolos elementos dos dous vectores en serie sería de ts = 6nt. As distintas fases da execución en función do tempo móstranse na táboa 2.

A pipeline aritmética
Imos mostrar agora cómo para segmenta-la operación anterior, isto é, facer que cada unha das seis fases necesarias para sumar cada par de elementos se realice en cada fase da cadea (pipeline). En cada paso desta cadea existe unha unidade aritmética separada deseñada para realiza-la operación que se desexa en cada fase. Unha vez que a fase A foi completada para o primeiro par de elementos, estes elementos poden ser desprazados ata a seguinte fase B mentres que o segundo par de elementos pódese mover cara a primeira fase (A). De novo, cada fase require t unidades de tempo. Polo tanto, o fluxo a través do pipeline pode ser representado como se mostra na figura1., onde cada unha das fases da suma segmentada se executa en función do tempo, tal e como se indica na táboa 3.

Como se pode ver, aínda son necesarias 6t unidades de tempo para completa-la suma do primeiro par de elementos, pero tamén se pode comprobar cómo o seguinte par de elementos está listo en tan só t unidades de tempo despois. E este patrón continúa para cada un dos pares seguintes. Isto significa que o tempo total, Tp, para realiza-la operación de forma segmentada sobre dous vectores de lonxitude n é:
Tp = 6t + (n-1)t = (n + 5)t
As primeiras 6t unidades de tempo son necesarias para enche-lo pipeline e para obte-lo primeiro resultado. Despois que se teña calculado o último resultado, xn + yn, o pipeline encóntrase baleiro.
Comparando as ecuacións para Ts e Tp, resulta evidente que (n+5)t < 6nt, para n>1. Polo tanto, a versión segmentada da suma resulta máis rápida cá versión secuencial por un factor case igual ó número de fases que existen no pipeline. Este é un exemplo que mostra por qué o procesamento vectorial resulta máis eficiente có procesamento escalar. Para valores grandes de n, a suma segmentada utilizando este pipeline é case seis veces máis rápida cá suma escalar.
No exemplo anterior, asumimos que a suma en punto flotante require seis etapas e que polo tanto utiliza 6t unidades de tempo. Sen embargo, en determinadas arquitecturas o número de fases necesario para realiza-la suma en punto flotante pode ser maior ou menor de seis. As operacións necesarias para realiza-la multiplicación de dous números en punto flotante tamén son lixeiramente diferentes ás necesarias para realiza-la multiplicación,malmente o número de fases necesario tamén adoita ser distinto. Ademais tamén poden existir pipelines para realizar operacións sobre números enteiros.

Rexistros vectoriais
Algúns ordenadores vectoriais, como o Cray Y-MP, conteñen rexistros vectoriais. Un rexistro de propósito xeral ou un rexistro de punto flotante contén un único valor. Sen embargo, os rexistros vectoriais conteñen no seu interior moitos elementos dun vector ó mesmo tempo. Por exemplo, os rexistros vectoriais do Cray Y-MP conteñen 64 elementos, mentres que os do Cray C90 conteñen 128 elementos. Os contidos destes rexistros poden ser enviados a (ou recibidos por) unha pipeline vectorial a razón dun elemento por paso temporal.
Rexistros escalares
Os rexistros escalares compórtanse da mesma forma cós rexistros de punto flotante, contendo un único valor. Sen embargo, estes rexistros configúranse de tal forma que poden ser utilizados por unha pipeline vertical. Neste caso, o valor do rexistro lese unha vez cada t unidades de tempo e introdúcese no pipeline, da mesma foma que cada elemento dun vector se introduce en cada paso na pipeline vectorial. Isto permite que os elementos dun vector poidan realizar operacións con elementos escalares. Por exemplo, para calcula-lo resultado da operación y = 2.5x, o valor 2.5 almacénase nun rexistro escalar e introdúcese na pipeline de multiplicación cada t unidades de tempo para ser multiplicado por cada un dos elementos de x e así obte-lo resultado no vector y.
Encadeamento
A figura 1 mostra o diagrama de funcionamento dun único pipeline. Como indicamos anteriormente, a maioría das arquitecturas vectoriais teñen máis dun pipeline, e en moitas ocasións presentan distintos tipos de pipelines.
Algunhas arquitecturas vectoriais proporcionan maior eficiencia ó permitir que a saída dun pipeline se poida encadear coa entrada doutro pipeline. Esta característica coñécese co nome de encadeamento e elimina a necesidade de almacena-lo resultado do primeiro pipeline antes de envialo ó segundo pipeline. A figura 2 demostra a utilización do encadeamento para o cálculo dunha operación vectorial: s = ax + y, onde x e y son vectores e a é unha constante escalar.
O encadeamento pode duplica-lo número de operacións en punto flotante que se realizan en t unidades de tempo. Unha vez que os pipelines de suma e multiplicación se encheron, pódense realizar unha operación de suma e outra de multiplicación en punto flotante (é dicir, un total de dúas operacións en punto flotante) cada t unidades de tempo.

Operacións de dispersión e agrupamento
Algunhas veces só son necesarios algúns dos elementos dun vector para realizar un cálculo. A maioría dos procesadores vectoriais están equipados para poder recolle-los elementos necesarios dun vector (unha operación de recollida) e colocalos xuntos nun vector ou nun rexistro vectorial. Se os elementos que se utilizan presentan un patrón de espaciado regular, o espaciado entre os elementos que se van recoller denomínase desprazamento ou stride. Por exemplo, se se queren extrae-los elementos:
x1,x5,x9,x13 ,..., x4(n-1)+1
do vector
(x1, x2, x3, x4, x5, x6,...,xn)
para realizar algún tipo de operación vectorial, dise entón que o desprazamento é igual a 4. Unha operación de dispersión reformatea o vector resultante para que os elementos se encontren espaciados correctamente. As operacións de dispersión e recollida tamén se poden utilizar con datos que non se encontran regularmente espaciados.
Procesadores vectoriais de rexistro vectorial
Se un procesador vectorial posúe rexistros vectoriais, os elementos do vector que se van procesar cárganse desde a memoria directamente no rexistro vectorial utilizando unha operación de carga vectorial. O vector que se obtén a partir dunha operación vectorial introdúcese nun rexistro vectorial antes de que se poida almacenar de novo na memoria mediante unha operación de almacenamento vectorial. Isto permite que se poida utilizar noutra operación sen necesidade de volver a le-lo vector, e tamén permite que o almacenamento se poida solapar con outro tipo de operacións. Neste tipo de ordenadores, tódalas operacións aritméticas ou lóxicas vectoriais son operacións de rexistro a rexistro, é dicir, só se realizan operacións vectoriais sobre vectores que xa se encontran almacenados nos rexistros vectoriais. Por este motivo, estes ordenadores coñécense como procesadores vectoriais de rexistro vectorial. A figura 3 mostra a arquitectura de rexistros e pipelines dun ordenador vectorial de rexistro vectorial. O número de etapas de cada pipeline móstrase entre parénteses dentro de cada pipeline.

Procesadores vectoriais memoria a memoria
Outro tipo de procesadores vectoriais permite que as operacións realizadas con vectores se alimenten directamente de datos procedentes da memoria ata os pipelines vectoriais e que os resultados se escriban directamente na memoria. Este tipo de procesadores coñécense co nome de procesadores vectoriais memoria a memoria. Dado que os elementos do vector necesitan vir da memoria en lugar de proceder dun rexistro, requírese máis tempo para conseguir que a operación vectorial comece a realizarse. Isto é debido en parte ó custo de acceso á memoria. Un exemplo de procesador vectorial memoria a memoria era o CDC Cyber 205.
Debido á capacidade de superpoñer o acceso á memoria e a posible reutilización dos vectores xa utilizados, os procesadores vectoriais de rexistro vectorial adoitan ser máis eficientes cós procesadores memoria a memoria. Sen embargo, a medida que a lonxitude dos vectores utilizados para un cálculo se incrementa, esta diferencia no rendemento entre os dous tipos de arquitectura tende a desaparecer. De feito, os procesadores vectoriais memoria a memoria poden chegar a ser máis eficientes se a lonxitude dos vectores é o suficientemente grande. Sen embargo, a experiencia demostrou que a lonxitude dos vectores adoita ser moito mais curta da necesaria para que esta situación chegue a producirse.
Bancos de memoria entrelazados
Para permitir un acceso máis rápido ós elementos vectoriais que se encontran almacenados na memoria, as memorias dos procesadores vectoriais acostúmanse a dividir en bancos de memoria. Os bancos de memoria entrelazados asocian de forma sucesiva as direccións de memoria con bancos sucesivos de forma cíclica. Desta forma, a palabra 0 almacénase no banco 0, a palabra 1 almacénase no banco 1, ..., a palabra n-1 almacénase no banco n-1, a palabra n no banco 0, a palabra n+1 no banco 1,..., etc., onde n é o número de bancos de memoria. Como sucede con moitas outras características de arquitectura de ordenadores, n é normalmente unha potencia de 2: n= 2k, onde k = 1, 2, 3, ou 4.
Un acceso a memoria (carga ou almacenamento) dun valor de datos nun banco necesita varios ciclos de reloxo para chegar a completarse. Cada banco de memoria permite só que se lea ou almacene un valor dos datos por cada acceso á memoria, mentres que se pode acceder a varios bancos de memoria de forma simultánea. Cando os elementos dun vector que se almacena nunha memoria entrelazada se trasladan ó rexistro vectorial, as lecturas repártense entre os bancos de memoria, de forma que un elemento vectorial é lido en cada banco por cada ciclo de reloxo. Se un acceso á memoria precisa de n ciclos de reloxo, entón n elementos dun vector poden ser lidos co mesmo custo do que sería necesario para un único acceso á memoria. Este procedemento é n veces máis rápido có necesario para realiza-lo mesmo número de accesos á memoria sobre un único banco.
Rendemento dos ordenadores vectoriais
Para as arquitecturas vectoriais máis usadas, o valor de t (o tempo necesario para completar unha fase da cadea ou pipeline) é equivalente a un ciclo de reloxo da máquina. Unha vez que o pipeline como o que se mostra na figura 1 se encheu, xérase un resultado para cada t unidades de tempo, é dicir, para cada ciclo de reloxo. Isto significa que o hardware é capaz de realizar unha operación de punto flotante por cada ciclo de reloxo.
Se k representa o número de t unidades de tempo que a mesma operación requiriría sobre unha máquina escalar (é dicir, o número de fases no pipeline), entón, o tempo necesario para executa-la mesma operación secuencial sobre un vector de lonxitude n é:
Ts = knt
e o tempo necesario para realiza-la versión segmentada é:
Tp = kt + (n-1)t = (n + k - 1)t
De novo se obtén que para n > 1, Ts > Tp
Tamén se necesita un tempo de arranque ou startup. Este é o tempo necesario para conseguir que a operación se realice. Sobre unha máquina secuencial, pode existir certa penalización como consecuencia do tempo necesario para prepara-lo lazo necesario para repeti-la mesma operación de punto flotante sobre un vector enteiro, xa que os elementos do vector tamén deben ser lidos desde a memoria. Se Ss é o número de unidades de tempo t que compoñen o tempo de arranque para a operación nun procesador secuencial, entón Ts, tamén debe incluír este tempo. Neste caso:
Ts = (Ss + kn)t
Nunha máquina segmentada, o fluxo desde os rexistros vectoriais ou desde a memoria cara ó pipeline tamén necesita inicializarse. A este tempo denominámolo Sp. Neste caso existe tamén outra penalización de kt unidades de tempo, necesarias para encher inicialmente o pipeline. Polo tanto Tp debe incluí-lo tempo de inicialización para a operación segmentada, é dicir:
Tp = (Sp+k)t+(n-1)t
ou
Tp = (Sp+k+n-1)t
A medida que a lonxitude do vector aumenta (é dicir, cando n tende a infinito), o tempo de inicialización vólvese desprezable en ámbolos dous casos. Isto significa que:
Ts -> knt
mentres que
Tp -> nt
Polo tanto, para valores grandes de n, Ts, é k veces maior que Tp.
Existe un número de factores adicionais para describi-lo rendemento dos ordenadores ou procesadores vectoriais. A continuación móstranse algunhas destas medidas:
Rn : Para un procesador vectorial, o número de Mflops que se poden obter ó operar sobre un vector de lonxitude n.
R¥: O número asíntótico de Mflops que se poden obter sobre un ordenador vectorial a medida que a lonxitude do vector se vai facendo maior. Isto significa que o tempo de inicialización se faría completamente desprezable. Cando os vectores son extremadamente longos, debería obterse un resultado do pipeline para cada t unidades de tempo, ou para cada ciclo de reloxo. Desta forma, o número de operacións en punto flotante que se poden completar nun segundo é de 1.0/t. Se se divide este resultado por un millón obtense o número de Mflops.
n½: A lonxitude, n, do vector tal que Rn é igual a R¥/2. De novo para vectores grandes, debería obterse un resultado á saída do pipeline por cada t unidades de tempo. Desta forma, n½ representa a lonxitude de vector necesaria para conseguir un resultado cada 2t unidades de tempo ou cada dous ciclos de reloxo.
Nv: A lonxitude, n, dun vector tal que realizar unha operación vectorial sobre os n elementos do vector resulta máis eficiente que executa-las n operacións escalares.
A figura 4 e a figura 5 mostran a relación existente entre estas cantidades para unha máquina vectorial na que t = 6 nanosegundos e Sp = 16t. Esta é unha representación teórica, xa que existen lixeiras variacións na curvatura da gráfica nos casos nos que n é un múltiplo da lonxitude do rexistro.
A táboa 4. proporciona algunhas das características de rendemento de diversos ordenadores vectoriais. Os valores de R¥ e de n½ son os que se obteñen para a multiplicación de tódolos elementos de dous vectores.
Programación de ordenadores vectoriais
Os ordenadores vectoriais poden realizar operacións en punto flotante sobre vectores de n elementos de forma máis eficiente que sobre n variables escalares. Para poder crear programas que maximicen o rendemento sobre estes ordenadores, é necesario organiza-los datos en forma de vectores e utiliza-las operacións vectoriais tanto como sexa posible.
Os deseñadores de ordenadores vectoriais a miúdo proporcionan compiladores con construccións adicionais á linguaxe deseñadas para axudar ó manexo de vectores ou de matrices. Estas construccións tamén axudan ó programador a pensar nun vector como nunha entidade única, en lugar de pensar nel como unha lista de elementos separados.
Os compiladores dos ordenadores vectoriais intentan converte-lo código escalar en operacións vectoriais (código vectorial) sempre que sexa posible. Esta operación denomínase vectorizar códigos, e neste caso, vectorización automática, cando é o propio compilador o que determina as áreas do programa que se poden vectorizar. Sen embargo, estes compiladores non coñecen, nin o programa, nin os datos utilizados, tan ben como o propio programador, polo que ás veces son incapaces de vectoriza-lo código do mesmo modo en que o faría o propio programador. Polo tanto, é recomendable introduci-las directivas apropiadas para indicar cáles son as operacións vectoriais que se desexan realizar, en lugar de que sexa o compilador o que as busque. A esta operación denomínaselle vectorización manual, e é a base do porting dun programa a un ordenador vectorial.

|
