|
Ordenadores Paralelos de memoria distribuída.
Os problemas de cálculo computacional que se adoitan encontrar nas aplicacións científicas e de enxeñería acostuman presentar unhas dimensións moi elevadas. Resolver estes problemas utilizando ordenadores convencionais pode consumir demasiado tempo de proceso e demandar demasiada cantidade de almacenamento. En moitos casos, os procesadores paralelos de memoria distribuída (DM-MIMD: MIMD son as iniciais de multiple instruction, multiple data) poden proporcionar tanto a potencia de cálculo como a cantidade de memoria necesaria para resolver este tipo de problemas. Arquitectura de Ordenandores DM-MIMD.
Arquitectura de ordenadores DM-MIMD
Un DM-MIMD é un ordenador paralelo no cal cada procesador ten acceso directo unicamente á súa memoria local. Os procesadores encóntranse interconectados mediante enlaces de comunicación, e os procesadores intercambian os datos en forma de mensaxes que se distribúen a través destes enlaces. Debido a que un DM-MIMD está formado por ordenadores MIMD, é posible executar múltiples programas en cada procesador de forma simultánea.
Os distintos tipos de ordenadores paralelos DM-MIMD pódense caracterizar atendendo a diversos factores como: a potencia dos procesadores, o tamaño da memoria, a velocidade das comunicacións entre os procesadores, a dispoñibilidade de medios de entrada/saída, e o patrón de interconexión entre os procesadores. Os ordenadores DM-MIMD poden estar formados por tan só dous procesadores ou por varios miles de procesadores. Estes procesadores poden estar conectados formando un anel, mallas bidimensionais ou formas toroidais, entre outras estructuras.
Grafos de interconexión.
Os nodos nos ordenadores DM-MIMD pódense representar como os nodos dun grafo determinado, e os enlaces utilizados nas comunicacións entre os procesadores encóntranse nos bordos deste grafo. A continuación móstranse algúns dos tipos de grafos máis importantes que se utilizan nos DM-MIMD comerciais.
Arrays, aneis e toroides
A figura 1 mostra os grafos máis sinxelos que se poden encontrar nos ordenadores DM-MIMD. O diagrama (a) representa unha matriz lineal de oito procesadores. Nesta distribución, un nodo ten un ou dous veciños máis próximos, dependendo de se se encontra nun dos extremos da matriz. Se se unen os extremos deste array, obtense un anel, tal como se mostra no diagrama (b). Neste caso, tódolos nodos teñen dous veciños.</span></p> <p><span class=">Os nodos tamén se poden conectar formando un array bidimensional de p1 x p2 elementos, ou unha malla de procesadores, como se mostra no diagrama (c). Neste caso p1 = 3 e p2 = 4, e cada nodo ten dous ou tres veciños, en función da súa posición na malla. Nunha malla con máis filas, un nodo pode ter ata catro veciños máis próximos. Estes veciños identifícanse polas súas posicións relativas e denomínanse veciños norte, sur, leste e oeste.
Se se conectan os nodos correspondentes ós extremos esquerdo e dereito e os correspondentes ós extremos superior e inferior dunha malla bidimensional, esta convértese nun torus tridimensional como se mostra no diagrama (d). Neste caso, tódolos nodos teñen catro veciños máis próximos.
Ó aumenta-la conectividade do grafo de oito procesadores, redúcese a distancia máxima que existe entre dous procesadores calquera do grafo. Nun DM-MIMD, isto tradúcese nunha reducción no tempo para realiza-las comunicacións entre procesadores. Así, nun array lineal, existen p-1 liñas entre os nodos 0 e o p-1, e este é o camiño máis longo entre calquera par de nodos. Este camiño móstrase representado pola frecha do diagrama (a) da figura 2. Se se conectan os bordos deste array para formar un anel, redúcese este camiño ata a metade. Se ademais se permite que exista comunicación en ámbolos dous sentidos (é dicir, se o grafo é bidireccional), o camiño máis longo encóntrase entre os nodos 0 e p/2, e este camiño percorre p/2 liñas de comunicación no diagrama (b) da figura 1. Na malla, o camiño máis longo entre nodos encóntrase entre as esquinas opostas (figura 2.(c)). Este camiño ten de lonxitude p1 + p2 - 2. Cando p = 8, o camiño máis longo entre os dous é catro, tanto para o anel coma para a malla. As vantaxes da malla son máis evidentes para un número de nodos maior. Por exemplo, o camiño máis longo nunha malla de dimensións 16 x 16 percorre 30 liñas de conexión, mentres que o camiño máis longo de 162 = 256 nodos percorre 128 liñas de conexión.
O torus permite unhas condicións aínda máis favorables. Pode interpretarse como un conxunto de p1 aneis horizontais de p2 nodos, cada un deles interconectados mediante p2 aneis verticais de p1 nodos cada un. Polo tanto, o camiño máis longo que debe percorrerse entre o nodo A e o nodo B é, para este exemplo, a distancia entre o anel vertical do nodo A e o anel vertical do nodo B, máis a distancia arredor deste anel ata chegar ó nodo B (figura 2(d)). Se cada anel pode ser percorrido en ámbolos dous sentidos, o camiño máis longo é p1/2 + p2/2. No toro 2 x 4, o camiño máis longo é tres. No toro de dimensións 16 x 16, esta distancia é 16.
Rendemento das comunicacións nos ordenadores DM-MIMD
A evolución dos ordenadores trouxo consigo unha gran mellora no seu rendemento. Igual que con calquera outro tipo de ordenador, o rendemento dos ordenadores DM-MIMD pódese representar de distintas formas, en función do número de Mflops que alcanza o benchmark do LINPACK, por exemplo. Ademais destas medidas de rendemento clásicas, o rendemento dun ordenados DM-MIMD está determinado pola velocidade das comunicacións de datos entre os nodos. A continuación móstrase cómo esta velocidade de comunicación pode afectar ó rendemento dos ordenadores DM-MIMD.
Paso de mensaxes entre nodos veciños.
Dise que existe transmisión de mensaxes entre dous nodos cando se executa un comando para enviar unha mensaxe no nodo emisor, e se executa un comando de recepción desta mensaxe no nodo receptor. O proceso exacto de paso de mensaxes que se realiza despois de executarse estes comandos depende de cada ordenador, pero adoita involucrar procesos de inicialización dos buffers de mensaxes en ámbolos dous nodos, así como o establecemento da ruta de comunicación entre eles, ademais da transferencia da mensaxe actual a través dos enlaces de comunicación.
Se b é o tempo necesario para prepara-lo hardware e o software necesario para transmitir unha mensaxe e t é o tempo empregado para enviar un bit de datos a través do enlace que une os dous nodos, o tempo necesario para enviar k bits de datos desde un nodo a un dos seus veciños máis próximos está dado pola expresión:
Tcomun = ß + kt
Normalmente, o tempo necesario para enviar unha mensaxe é moito maior có tempo necesario para realizar unha operación en punto flotante. En particular, b > > w ³ t, onde w é o tempo necesario para realizar unha operación en punto flotante. A táboa 1 mostra os valores de b, w e t e a relación b/w para algúns ordenadores DM-MIMD. Tódolos tempos que se mostran están representados en microsegundos. Nesta táboa, w representa o tempo necesario para realizar unha multiplicación en punto flotante de dobre precisión (8 bits). A primeira columna mostra o ano en que se presentou a máquina, aínda que algúns datos foron modificados nos modelos mellorados. A última columna da táboa mostra a velocidade de reloxo de cada procesador.
Cando a lonxitude da mensaxe é inferior a 100 bits, no iPSC/2 e no iPSC/860 utilízase un protocolo especial para transmitir mensaxes. Nestes casos, os valores de b encóntranse reducidos. Os valores de b para estas mensaxes pequenas móstranse entre parénteses dentro da táboa.
A táboa 1. mostra que tanto a computación como a comunicación co veciño máis próximo melloraron en rendemento a medida que apareceron novos ordenadores. Sen embargo, aínda se cumpre que b > > t. Isto significa que é mellor enviar moitos bits de datos utilizando moitas mensaxes pequenas. Os programas que se van executar sobre ordenadores DM-MIMD deben ser deseñados tendo isto presente.

Paso de mensaxes entre nodos arbitrarios
Cando os nodos de envío e de recepción non son os veciños máis próximos, o custo da transmisión dos datos depende completamente de cómo os nodos intermedios que se encontran ó longo do camiño que debe segui-la mensaxe manexan esta transferencia de mensaxes. Os primeiros ordenadores DM-MIMD, como o iPSC/1, tiñan un único procesador por nodo. Este procesador encargábase non só do cálculo, senón tamén da comunicación, así que as mensaxes que chegan a un nodo interrompen calquera operación que estea realizando, incluso se ese nodo non é o receptor da mensaxe. Os últimos modelos de ordenadores DM-MIMD, a partir do iPSC/2 e do nCUBE/2, teñen hardware específico separado para realiza-los cálculos e as comunicacións, e poden operar de forma independente. As mensaxes que pasan a través dun nodo procésanse mediante un procesador de comunicacións, de forma que os cálculos que se estean realizando non se ven afectados. Sen embargo aínda segue sendo máis custoso enviar unha mensaxe desde un nodo a outro que se encontre distante, que envia-la mensaxe a nodos que sexan veciños, xa que a mensaxe vai sufrindo pequenos atrasos ó pasar por cada un dos procesadores intermedios.
O rendemento nas comunicacións interprocesadores incrementouse coa chegada do wormhole routing. No wormhole routing (como o implementado nos ordenadores de Intel), envíase un paquete "preliminar" desde o emisor ó receptor para configurar e reservar unha canle de comunicación a través dos nodos intermedios. A mensaxe pasa entón a través desa canle sen atrasos. O overhead debido a este mecanismo de switching de circuítos é difícil de medir, pero parece representar só unha pequena porcentaxe do tempo total de comunicación nas novas máquinas (como nos ordenadores de Intel: Delta e Paragon). Polo tanto, en ordenadores con wormhole routing, o tempo necesario para enviar unha mensaxe entre nodos distantes é aproximadamente o mesmo có tempo necesario para envialo a nodos veciños.
A velocidade da comunicación entre nodos reflíctese no ancho de banda de comunicación dunha máquina: cando a velocidade de transferencia é rápida, transmítese un maior número de bits de datos por segundo. A táboa 2 mostra o ancho de banda de comunicación de varios multiprocesadores medido en función do tamaño da mensaxe (8, 1024 e 8192 Kbytes) e a distancia que debe viaxar no ordenador. Unha mensaxe de tipo "1 hop" representa unha mensaxe entre os veciños máis próximos, e unha mensaxe "6 hop" é unha mensaxe que pasa a través de cinco nodos intermedios que se encontran entre o emisor e o receptor. As máquinas que non posúen procesadores separados de comunicación ou que non permiten facer wormhole routing (como o iPSC/1 e o nCUBE/1) sofren unha forte degradación no seu ancho de banda cando o número de hops aumenta desde un ata 6. Os outros ordenadores demostran pouca ou ningunha diminución no ancho de banda de comunicación entre nodos distantes.

Paso de mensaxes longas.
Na expresión que mostramos Tcomun, o tamaño da mensaxe só aparece dentro do termo kt. Sen embargo, na maioría dos ordenadores o tempo de arranque (startup) tamén adoita ser función do tamaño da mensaxe.
Tal como se recolle na táboa 1., o tempo de startup redúcese no iPSC/2 e no iPSC/860 cando k é moi pequeno. Nalgúns ordenadores b tamén aumenta cando o tamaño da mensaxe é moi grande. Neste caso, a mensaxe pode ser enviada como un conxunto de paquetes máis pequenos en vez de cómo unha mensaxe única máis grande, e o envío de cada paquete individual só engade unha pequena cantidade de custo adicional á comunicación completa. A pesar de que a maioría do tempo de arranque (startup) se utiliza para o primeiro paquete, o efecto de dividi-la mensaxe en paquetes (empaquetamento) adoita facerse visible nunha representación na que se mostre o tempo de comunicación entre dous nodos fronte ó tamaño da mensaxe. A figura 3 mostra esta representación para dous ordenadores hipotéticos, un que divide as mensaxes grandes en paquetes e outro que non as divide. A liña sólida mostra Tcomun = b + kt representada en función de t cando b = 500 e t = 1 para un ordenador que non realiza empaquetamento. Como era de esperar, esta gráfica é unha función lineal de k. A pendente desta recta é t, e o seu punto de corte co eixe Y coincide con b.
Como contraste, a liña punteada da figura 3 mostra a forma característica da curva cando a mensaxe se divide en paquetes de 250 bits de lonxitude. As liñas sólidas e punteadas con colineais ata que k = 251. Neste punto, o ordenador que realiza empaquetamento divide a mensaxe en dous paquetes: un con 250 bytes e outro co byte restante. O repentino salto na cantidade de tempo reflicte o overhead necesario para envia-lo segundo paquete; a curva aumenta a continuación de forma lineal mentres que o segundo paquete crece ata os 250 bytes. Cando k = 501, a curva mostra outro salto, debido a que é necesario enviar un terceiro paquete. A pesar de que as gráficas obtidas a partir de resultados experimentais non adoitan ser tan "suaves" como os mostrados na figura 3, a forma en chanzo da curva punteada tende a aparecer claramente ó realiza-las medidas en ordenadores que presentan un overhead de empaquetamento medible. En particular, pódese observar este comportamento nos programas reais nos que interveñan mensaxes de lonxitude elevada. O tamaño do paquete adoita ser moderadamente grande: no iPSC/1 é de 1024 bytes, no Delta é de 476 bytes, e no Paragon é de 1792 bytes.
O overhead debido ó empaquetamento de mensaxes é evidente nos anchos de banda que se mostran na táboa 2. En concreto, o empaquetamento das mensaxes significa que non se observa o aumento lineal no ancho de banda que se esperaría a partir da dependencia lineal de Tcomun co tamaño da mensaxe. Este efecto aparece nos datos de 1-hop do nCUBE/2. Cando o tamaño da mensaxe aumenta desde 8 ata 1024 bytes (por un factor de 128), o ancho de banda na comunicación co veciño máis próximo aumenta desde 50 Kb/s ata 1289 Kb/s (un factor de tan só 26). Ó aumenta-lo tamaño da mensaxe desde 1024 ata 8192 (un factor de 8) só aumenta o ancho de banda nun factor de 1.2. Sen embargo, incluso aínda que se perda eficiencia no proceso de empaquetamento, o incremento en ancho de banda en conxunto co aumento da lonxitude da mensaxe demostra que é xeralmente preferible pasar só unha poucas mensaxes longas que pasar moitas mensaxes pequenas.

A contención nos enlaces de comunicación.
Un último aínda que moi importante aspecto do rendemento nas comunicacións entre nodos é o número de mensaxes que percorren unha determinada liña de comunicación nun momento dado. Cando máis dunha mensaxe atravesa un circuíto de comunicación dado, dise que estas mensaxes compiten por ese circuíto. Os efectos desta contención dependen do ordenador no que se produzan. Por exemplo, se nodos veciños dun iPSC/1 mandan mensaxes a cada un de forma simultánea, o tempo necesario para o intercambio de datos é aproximadamente 2Tcomun: nin os tempos de inicialización (startup) nin as transferencias de datos a través do enlace poden solaparse. Sen embargo, os últimos modelos de ordenadores paralelos si permiten que as inicializacións para a emisión e recepción de mensaxes se solapen no tempo, e o tempo necesario para esta transmisión (denominada head-to-head send) aproxímase a b + 2kt.
O problema da contención complícase cando as mensaxes que se envían entre varios nodos toman camiños descoñecidos a través do ordenador paralelo. Por exemplo, supoñamos que unha mensaxe de k-bytes se encontra atrasado, mentres que un conxunto de mensaxes de q bytes pasa a través dun enlace cara ó seu camiño. Daquela, o tempo que necesita esta mensaxe para chegar ó seu destino vese incrementado nun factor qt. Se q é grande, este atraso pode ser substancial. A contención prodúcese nun enlace de comunicación sempre que a cantidade de datos total que debe pasar a través del supera o ancho de banda dese enlace.
O efecto global da contención sobre o rendemento dun programa paralelo resulta moi difícil de predicir, pero, en xeral, resulta conveniente programar de forma que se eviten as posibles contencións.
Rendemento global de ordenadores DM-MIMD
O rendemento global dos ordenadores paralelos de tipo DM-MIMD está determinado non só polo seu rendemento nas comunicacións senón tamén polo seu rendemento computacional. A táboa 1 mostraba que, igual que sucedía co tempo necesario para enviar unha mensaxe, o tempo necesario para realizar unha multiplicación en punto flotante de dobre precisión tamén diminuíu substancialmente con cada nova arquitectura. Isto tamén é certo para o tempo necesario para calquera outra operación en punto flotante. Así pois, dado que a velocidade de comunicación e a velocidade de cálculo aumentaron, debemos supoñer que un programa paralelo se executará de forma máis rápida nun modelo novo de ordenador DM-MIMD que nun modelo anterior.
Sen embargo, a velocidade de execución no é o único ingrediente necesario para mellora-lo rendemento. A Lei de Amdahl dinos que o speedup dun programa paralelo se encontra limitado pola fracción de tempo que se consome en realizar operacións que non se poden executar en paralelo. Por extensión, o speedup tamén se encontra limitado polo tempo necesario para realiza-la comunicación de datos. Dado que non se realizan comunicacións cando un programa se executa nun único nodo, a comunicación constitúe unha parte do overhead da implementación paralela.
Para poder aprecia-lo efecto da comunicación de datos sobre o speedup, podemos supoñer que temos un programa secuencial con cálculos perfectamente paralelizables. Se non se necesitase ningún tempo para realiza-las comunicacións entre os nodos, o tempo necesario para executa-lo programa sobre p sería só o tempo necesario para executa-lo programa nun único nodo e dividido por p, é dicir, Tp = T1/p. Se se necesita realizar comunicacións de datos, e as comunicacións e os cálculos non se poden solapar no tempo, o tempo necesario para realiza-lo cálculo en p-nodos aumenta un factor Tc, necesario para realiza-las comunicacións, de forma que
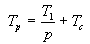
Tendo en conta que o speedup para un programa paralelo se define como
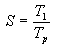
Para poder examinar máis facilmente os efectos da comunicación sobre o speedup, podemos considera-lo valor recíproco
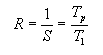
Para o noso programa "perfecto" con comunicacións de datos, este recíproco convértese en
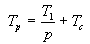
Se o custo de comunicacións é nulo, entón R = 1/p e o programa presenta un speedup perfecto S = p. En calquera outro caso, o recíproco do speedup está determinado pola relación Tc/T1. Canto maior sexa o custo debido ás comunicacións en comparación co custo computacional (ou de cálculo), maior será o valor de R. Polo tanto, canto maior sexa a relación dos custos de comunicación en comparación cos custos de computación, menor será o speedup S. A última columna da táboa 1. mostra a relación do tempo para a inicialización da mensaxe b co tempo necesario para realizar unha operación de multiplicación en punto flotante w. Estes datos mostran claramente que co incremento na velocidade de cálculo, produciuse un marcado incremento na relación entre o custo de comunicación e o custo de cálculo. Polo tanto, aínda que podemos esperar que o noso programa paralelo se execute moito máis rapidamente sobre estes novos ordenadores, tamén podemos esperar que o speedup que obteñamos sexa inferior.
O incremento na relación entre comunicacións e cálculo cambiou recentemente debido á mellora substancial nas capacidades de comunicación dos novos ordenadores DM-MIMD. Entre o iPSC/1 e o Paragon (SUN-MOS), a relación b/w creceu nun factor de 66. Ó mesmo tempo, o ancho de banda das comunicacións para as mensaxes de 8192 bytes de lonxitude aumentou nun factor de 164.
Para comproba-las repercusións que estas melloras produciron é necesario examinar algúns exemplos computacionais. Xa que non existen datos estándar do speedup para un gran número de ordenadores, é necesario examina-lo speedup dun programa numérico paralelo en comparación co rendemento pico teórico do ordenador; aínda así, este é un tipo de medida da eficiencia pouco satisfactoria, xa que mestura aspectos relacionados coa programación eficiente sobre un único procesador con aspectos de programación paralela, pero de ningún modo nos ofrece unha información precisa sobre as tendencias do speedup, como se comenta a continuación.
O programa paralelo que se empregou consiste na solución do sistema lineal máis grande que pode caber nun ordenador DM-MIMD dado: Highly Parallel Computing benchmark (Dongarra, 1994). A táboa 3 mostra o tamaño do sistema n (número de ecuacións), os megaflops medidos para a solución deste sistema e o rendemento pico teórico dese ordenador para operacións aritméticas de 64 bits. A columna final mostra a relación entre o rendemento medido e o rendemento pico teórico. Os datos móstranse para ordenadores conp = 1, 2 e 8 nodos.


O iPSC/860 foi un dos primeiros ordenadores DM-MIMD co rendemento suficiente para resolver problemas científicos realistas sobre un número moderado de procesadores. Tanto o iPSC/860 como o Delta utilizan o procesador i860. Entre o iPSC/860 e o Delta, a relación b/w (para mensaxes longas) diminuíu, mentres que o ancho de banda para as mensaxes aumentou. Como se mostra na táboa 3, o rendemento global do Delta é incluso mellor que o iPSC/860, especialmente ó aumenta-lo número de procesadores.
Se comparamos estes dous ordenadores co nCUBE/2 observamos que a mellora nas comunicacións non é enteiramente responsable do rendemento paralelo. Os datos que se obteñen para problemas de dimensións similares cando p = 8 mostran que, mentres que o rendemento pico teórico do Delta é 17 veces o do nCUBE/2, o rendemento experimental aumenta tan só nun factor de 14. Esta proporción cúmprese a pesar do feito de que o ancho de banda da comunicación para unha mensaxe de 8192 bytes é case oito veces maior no Delta que no nCUBE/2. Isto é debido en parte ó aumento en 8 veces da relación entre b/w entre os dous ordenadores, pero está aínda máis influenciado pola dificultade en programa-lo procesador i860. Os datos p = 1 mostran que o rendemento pico teórico é substancialmente máis realista para o nCUBE/2 que para os ordenadores baseados no i860.
A principal vantaxe dos ordenadores DM-MIMD reside nas súas memorias distribuídas de elevada capacidade e na súa potencia de cálculo cumulativo. O Highly Parallel Computing benchmark demostra o potencial total dun ordenador paralelo para a resolución de sistemas lineais. Este benchmark indícano-los Gflops obtidos ó resolve-lo sistema lineal máis grande que pode caber no ordenador utilizando calquera método numérico estable. A táboa 4 mostra estes rendementos en Gflops e as dimensións dos problemas para algunhas das máquinas que acabamos de examinar, ó utilizar 128 nodos. En comparación, un Paragon (OSF) de 296 nodos é capaz de obter 12.5 Gflops ó resolver un problema de 29400 ecuacións lineais.
Resumindo, o rendemento dun ordenador DM-MIMD depende dunha gran variedade de factores que interactúan entre si. O rendemento pico teórico depende de aspectos estándar como a cantidade de memoria e a velocidade do procesador. Cando se deben realizar transferencias de datos, tamén está determinado polo ancho de banda das comunicacións. O speedup que se pode alcanzar depende sobre todo do grao en que o programa secuencial se pode dividir en tarefas independentes e paralelas. Tamén depende do número e tamaño das mensaxes que se transmiten e da relación entre os tempos de comunicación e de cálculo. Resulta moi difícil poder predici-lo rendemento dun programa real estudiando calquera destes aspectos de forma separada, a pesar de que os datos de rendemento que acabamos de mostrar demostran que os ordenadores paralelos DM-MIMD poden resultar unha ferramenta moi potente para tratar moitas tarefas de cálculo intensivo.
|
